from 01.01.2019 to 01.01.2023
Belgorod, Belgorod, Russian Federation
UDC 624.071.322
Russian Classification of Professions by Education 08.00.00
Russian Library and Bibliographic Classification 302
Russian Trade and Bibliographic Classification 5414
The main problem of reinforced flexible structures made of cellular concrete is a rather low specific adhesion at the border of the reinforcement with concrete. This negatively affects the pulling out of the reinforcement from the porous mass and leads to premature loss of the bearing capacity of the structure as a whole. The underestimation of the significant potential of the unused bearing capacity of the structure when using traditional reinforcement provides for the need to improve approaches to the reinforcement of flexible cellular concrete structures. Efficient reinforcement of cellular concrete structures is proposed to be carried out with reinforcing elements with a developed lateral surface - steel toothed belts, which significantly increase the contact area and qualitatively improve contact conditions. At the stage of computational justification, the results of an experimental study of the strength and deformability of samples of innovative reinforcing elements of steel toothed belts with various configurations of longitudinal perforation, which help to reduce the metal consumption of cellular concrete structures operating in bending, and directly improve their functional characteristics - thermal resistance and wave conductivity, are analyzed. The revealed variations in the physical and mechanical properties of reinforcement due to the changing pattern of its longitudinal perforation and the average characteristics of reinforcement used in the design analysis of reinforced cellular concrete structures are used to propose practical approaches to normalizing the values of characteristics and technologies for calculating reinforced cellular concrete structures
reinforced cellular concrete, cellular concrete bending structures, band reinforcement, steel toothed belt, strength and deformability of steel gear band, two-line diagram of steel
Введение. Проблема недостаточно полного включения поверхности арматуры в работу конструкции наиболее часто встречается при проведении экспериментальных исследований, изгибаемых ячеистобетонных конструкций [1]. Изгибаемые ячеистобетонные элементы принято армировать либо дисперсно, путем распределения по объему большого количества стержней малого диаметра, либо дискретно - отдельными арматурными элементами. Дискретное армирование ячеистобетонных конструкций однозначно имеет преимущества перед дисперсным за счет более технологичного локализованного распределения армирующих элементов в объеме пористой конструкции, а также их большего включения в совместную работу бетона и арматуры [2]. Но при этом, основной проблемой изгибаемых ячеистобетонных конструкций со стержневым армированием является достаточно низкое удельное сцепление на границе арматуры с бетоном, негативно влияющее на выдергивание арматуры из пористого массива и приводящее к преждевременной потере несущей способности конструкции в целом. Недооцененность существенного потенциала неиспользованной несущей способности конструкции при применении традиционного армирования, предусматривает необходимость совершенствования подходов к армированию изгибаемых ячеистобетонных конструкций [3].
Эффективное армирование ячеистобетонных конструкций предлагается осуществлять арматурными элементами с развитой боковой поверхностью – стальными зубчатым лентами СЗЛ [4]. Армирование стальными зубчатыми лентами позволяет существенно повысить площадь контакта и качественно улучшить контактные условия на границе бетон-сталь, обеспечивающие:
- лучшее сцепление армирующего элемента с ячеистым бетоном конструкции [5];
- лучшее использование прочности армирующего элемента в работе конструкции;
- большую дисперсию армирования, влекущую большую жесткость конструкции;
- большую долговечность, надежность и безопасность ячеистобетонного армированного изгибаемого элемента [6].
Будучи инновационным и, в этой связи, малопредставленным в нормах, армирующим элементом, СЗЛ нуждаются в экспериментальном исследовании физико-механических свойств, факторов действительной работы в составлен армированной конструкции и нормировании параметров, влияющих на прочность и деформативность армируемой конструкции, полагаемых в основу планируемой инженерной методики рационального проектирования армоячеистобетонных изгибаемых конструкций [7].
Методика. Для обоснования достоверности выдвинутых научных гипотез и проверки результатов численных исследований [8] эксперимента выполнена часть планируемой программы экспериментальных исследований, в части испытания арматурного элемента СЗЛ на разрыв согласно ГОСТ 1497-84 «Металлы. Методы испытания на растяжение». Работа выполнена с использованием оборудования центра коллективного пользования БГТУ им. В.Г. Шухова в составе проекта Пр-18/22 программы Приоритет 2030.
Основная часть. Проектирование элементов обязательно включает этап расчетного обоснования, в связи с чем необходимо установить фактические физико-механические характеристики предлагаемых арматурных элементов в широкой номенклатуре варьируемого поперечного сечения, определяющего разнообразия арматуры под различные проектные задачи [9]. В настоящей работе обобщаются и анализируются результаты экспериментального исследования прочности и деформативности образцов СЗЛ, обладающих различными конфигурациями продольной перфорации, определены усредненные характеристики арматуры, используемые при расчетном анализе армированных ячеистобетонных конструкций, предложена практические подходы к нормированию величин характеристик и технологий расчета совершенствованием нормативной нелинейной методики, выявлены вариации физико-механических свойств арматуры в связи с изменяющейся схемой ее продольной перфорации.
Перед проведением испытаний образцов были определены методические подходы к классификации нового предлагаемого класса арматурных элементов – СЗЛ [10]. Экспериментальное определении физико-механически характеристик проводилось на шести вариантах образцов варьирующейся продольной перфорации (рис. 1), маркированных следующим образом:
ШС.ШО.ШС.ШО.ШС.ШО.ШС-О(З)-ДлО.ДлП ,
где ШС, ШО… — ширины (мм) чередующаяся стальных фрагментов и отверстий слева-направо вдоль поперечного сечения образца;
О(З) — отверстие без зуба (О) или с зубом (З) — отогнутой вокруг короткой стороны стальной пластины в отверстии;
ДлО, ДлП — длина отверстия (мм), длина стальной перемычки между отверстиями, соответственно, вдоль продольного сечения образца.

Рис. 1. Образцы СЗЛ изменяемой продольной перфорации (слева-направо: серия 6 (5.5.5.5.5.5.5-О-20.5), серия 5 (5.5.5.5.5-О-20.5), серия 4 (10.5.10-О-20.5), серия 3 (7,5.10.7,5-О-20.5), серия 2 (5.5.5-О-20.5), серия 1 (без перфорации, ширина 25 мм)
Стальные ленты для испытаний выполнены в виде типовых пропорциональных плоских образцов длиной 500 мм различной ширины в зависимости от конфигурации одиночной, двойной и тройной перфорации и ее размеров. Материал образцов лент - оцинкованная сталь 1 сорта марки 08пс класс цинкового покрытия 100 толщина металла 1 мм по ГОСТ 14918-2020 «Прокат листовой горячеоцинкованный». Ленты изготовлены немеханическим способом обработки металла, для их производства использовалась технология лазерной резки металла, позволяющая достигать высочайшей точности разреза, что подтверждается натурными замерами полученных образцов – погрешность геометрических размеров минимальна и не превышает предельно допустимую [11].
Испытания выполнялись на универсальной разрывной испытательной машине серии WEW-600D для установления фактических характеристик механических свойств образцов: модуля упругости, физического и условного предела текучести, временного сопротивления, относительного равномерного удлинения [12].
Внешний вид испытанных образцов СЗЛ изменяемой продольной перфорации серии 6 (5.5.5.5.5.5.5-О-20.5), серии 5 (5.5.5.5.5-О-20.5), серии 2 (5.5.5-О-20.5), серии 1 (без перфорации, ширина 25 мм) представлены на рисунке 2. Величина относительного удлинения является основным показателем пластичности исследуемой стали при испытании на растяжение. Относительное удлинение, зарегистрированное при разрушении образцов, составляет порядка 20% от начальной расчетной длины образца.
Физико-механические свойства образцов серии 2 (5.5.5-О-20.5) по результатам испытаний представлены на рисунке 3 в форме диаграммы σ – ε. Также приведены параметры усредненной по образцам двухлинейной диаграммы по п. 6.2 СП 63.13330.2018, усредненные прочности Ry и Rs и начальный модуль деформации E.

Рис. 2. Внешний вид образцов лент изменяемой продольной перфорации до и после разрыва
Физико-механические свойства образцов серии 2 (5.5.5-О-20.5) по результатам испытаний представлены на рисунке 3 в форме диаграммы σ – ε. Полученная экспериментальная диаграмма σ – ε является характерной для пластичных материалов, что позволяет ее привести к упрощенной двухлинейной диаграмме поведения стали – диаграмме Прандтля. А также выделить на ней основные ключевые точки (нижний рис. 3). Крайняя верхняя точка начального прямолинейного участка диаграммы определяет предел пропорциональности стали порядка 290МПа, до нее зависимость напряжений от относительных деформаций линейна: напряжения прямо пропорциональны деформациям, что характерно для большинства материалов и описывается законом Гука. Максимальное напряжение, до которого в материале не возникает пластических деформаций определяет предел упругости стали – 340 МПа. После прохождения предела пропорциональности, зависимость между напряжениями и деформациями меняется, и закон Гука становится неактуальным и материал начинает вести себя пластично. Линия, движущаяся параллельно оси деформаций ε, и образующая горизонтальный участок диаграммы представляет площадку текучести и определяет предел текучести стали равный 327 МПа. Максимальное напряжение, которое возникает в образце перед началом разрушения определяет предел прочности стали или временное сопротивление разрыву составляет 361 МПа (верхний рис. 3). В результате обработки данных, установлено расчетное сопротивление металла Ry =327 МПа, начальный модуль деформации E=155714 МПа. Также на рис. 3 приведены параметры усредненной по образцам двухлинейной диаграммы по п. 6.2 СП 63.13330.2018, усредненные прочности Ry и Rs и начальный модуль деформации E.
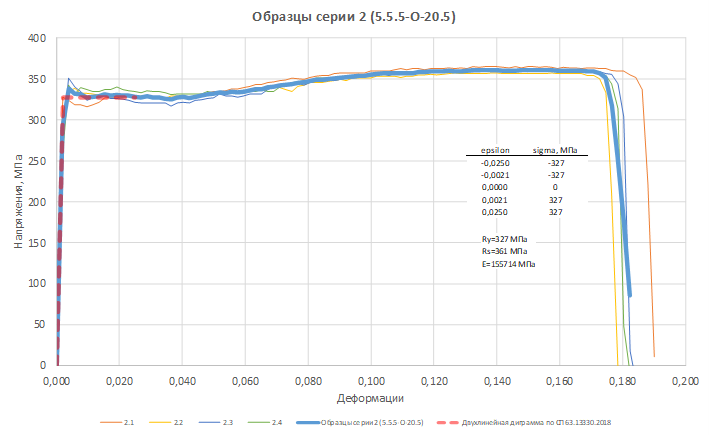
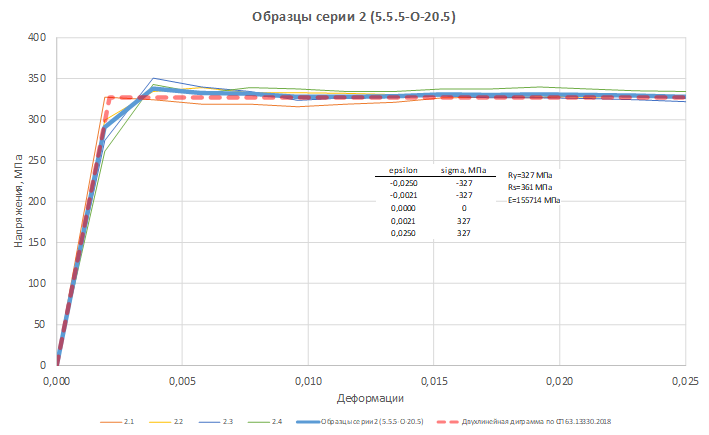
Рис. 3. Физико-механические свойства образцов серии 2 (5.5.5-О-20.5): вверху — диаграмма стали образца в диапазоне деформаций от 0 до разрушения, внизу — то же в диапазоне деформаций от 0 до Es2; параметры усредненной по образцам двухлинейной диаграммы по п. 6.2 СП 63.13330.2018, усредненные прочности Ry и Rs и начальный модуль деформации E
Разработка инженерной методики рационального проектирования СЗЛ требует экспериментального определения и математического моделирования краевых процессов, происходящих у отверстий – ослаблений сечения СЗЛ, получаемых при их производстве. Приступив к формулировке научно-теоретических положений инженерной методики после обработки результатов численных исследований арматурных элементов автором были выявлены некоторые необходимые для инженерной методики регрессионные зависимости параметров двухлинейных диаграмм состояния стального элемента от приведенной площади его поперечного сечения (рис. 4), в которой неравнозначно учитывались вырезы по ширине ленты с учетом количества вырезов и их расположения. Предполагаемая зависимость между количеством и размерами отверстий, общей площадью поперечного сечения, количеством краевых и центральных зон сохранения элементом поперечного сечения и действующими в элементе усилиями при общем центральном растяжении, как армирующем элементе изгибаемой балки, была сформулирована в виде коэффициента концентрации напряжений, изменяемого по ширине элемента. [13].
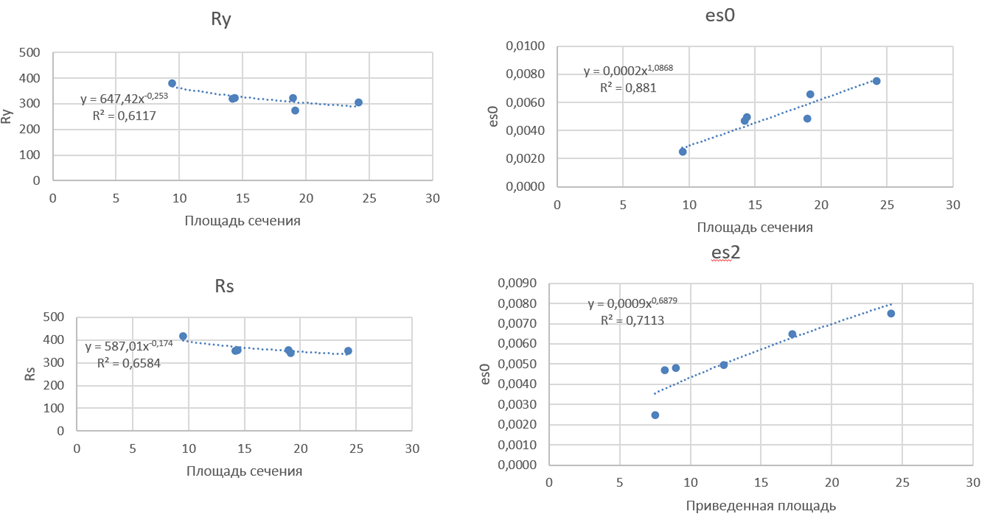
Рис. 4. Графики зависимости параметров (Ry – левый верхний, Rs – левый нижний, Es0 – правый верхний, Es2 –правый нижний) двухлинейных диаграмм состояния СЗЛ от приведенной площади поперечного сечения с учетом коэффициента напряжения
Выявленные зависимости параметров представлены графиками элементарных степенных функций. Зависимость расчетного сопротивления Ry от приведенной площади поперечного сечения (левый верхний график рис. 4) описывается убывающим графиком степенной функции с действительным показателем степени: при увеличении площади поперечного сечения образца отмечается снижение расчетного сопротивления стали. Зависимость временного сопротивления Rs от приведенной площади поперечного сечения (левый нижний график рис. 4) также представляет аналогичную степенную функцию, описанную убывающим графиком, по которому при увеличении площади поперечного сечения образца отмечается снижение временного сопротивления стали разрыву. Зависимость параметра остаточных деформаций Es0 от приведенной площади поперечного сечения (правый верхний график рис. 4) представлена возрастающим графиком степенной функции с иррациональным показателем, где при увеличении площади поперечного сечения образца отмечается рост остаточных деформаций. Зависимость относительных деформаций Es2 от приведенной площади поперечного сечения (правый нижний график рис. 4) описана возрастающим графиком степенной функции с иррациональным показателем, по которому видно, что с увеличением площади поперечного сечения также отмечается возрастающие относительные деформации стального образца. Коэффициент детерминации (R2) всех графиков находится в диапазоне до 1: от 0,6117 до 0,881, что отражает допустимое качество регрессионной модели, описывающей связь между зависимой и независимыми переменными модели.
Отклонения изменений от линейного как раз и определяются разнообразием размера и расположения отверстий, формирующих индивидуальный для каждого элемента набор концентраторов напряжения, способствующих перераспределению усилий и требующих учета при построении модели. Вырезы примыкающие к краю сечения оценивались как концентратор напряжения в 2 раза менее значимый, чем вырезы, расположенные в центре [14].
Что также подтверждается выполнением нелинейного физического расчета в специализированном софте ПК ЛИРА-САПР 2022 (рис. 4): в точках контура отверстий напряжения разнятся порядка 2 раз, что и послужило первым приближением к оценке влияния концентраторов через приведенную площадью. Для определения уточненного коэффициента влияния концентратора напряжений при учете положения и размеров выреза отверстий по длине лент планируется проведение ряда оптимизационных расчетов [15]. Конечной целью эксперимента является определение параметров физико-механических характеристик армирующего элемента в нелинейно-деформированной постановке прямой задачи, определяемой двухлинейной диаграммой материала в соответствии с п. 6.2 СП 63.13330.2018.

Рис. 4. Оценка влияния концентраторов напряжений в арматурных элементах через приведенную площадь лент, МПа
Выводы.
Элементы СЗЛ могут быть аппроксимированы двухлинейной диаграммой стали, используемой при расчете армированных ячеистобетонных изгибаемых элементов по прогрессивной нелинейно-деформируемой модели как с использованием положений СП 63.13330.2018, так и в специализированном ПО, методом конечных элементов.
Результаты испытаний образцов варьируемых параметров перфорации в продольном направлении продемонстрировали небольшую значимость геометрических характеристик перфорации на прочность СЗЛ. Характеристикой, определяющей прочность элемента в составе ячеистобетонной конструкции является чистая площадь сечения, а геометрические характеристики перфорации, предположительно, имеют существенное влияние на прочность сцепление элемента с ячеистым бетоном в массиве конструкции, что оказывает влияние на величину усилий продергивания арматуры и коэффициент ее конструктивного использования в элементе.
Получаемые перфорацией элемента отверстия приводят к повышению ресурсоемкости элемента за счет некоторого количества неиспользуемого удаляемого материала. Рациональным направлением совершенствования СЗЛ является недорез отверстия с оставлением одной из граней отверстия нетронутой, выгибом стального фрагмента в зуб, и предполагаемым повышением прочности сцепления с бетоном за счет усложнения напряженно-деформированного состояния элемента и снижения абсолютных значений касательных напряжений на поверхности арматуры.
Использование алгоритмов и методик, результатов численных и экспериментальных исследований позволят верифицировать область рационального использования инновационных армирующих элементов и в конечном итоге сделать предложение к совершенствованию строительных норм в части СП 63.13330.2018 «Бетонные и железобетонные конструкции» и СП 20.13330.2016 «Нагрузки и воздействия» для рационального проектирования ячеистобетонных изгибаемых элементов прямоугольного поперечного сечения произвольных размеров и армирования, раскрывающих перспективы практического использования при проектирования конструкций домокомплектов малоэтажных зданий, обеспечивающих полный переход на использование ячеистого бетона в ограждающих и несущих конструкциях и возведение энергоэффективных зданий с замкнутым тепловым контуром экономически конкурентоспособного ценового уровня.
1. Makarichev V.V., Mileikovskaya K.M. Research of reinforced structures made of cellular concrete. [Issledovanie armirovannyh konstrukcij iz yacheistyh betonov]. M.: Gostroizdat, 1963. 99 p. (rus).
2. Efimov O.I., Zamaliev F.S., Laskov N.N., Al-hasnavi Ya.S.G. To assess the strength of bent steel-concrete elements made of cellular concrete reinforced with a cold-bent profile. [K ocenke prochnosti izgibaemyh stalebetonnyh elementov iz yacheistogo betona, armirovannyh holodnognutym profilem]. Construction mechanics and calculation of structures. 2021. No. 6 (299). Pp. 7-12. DOI:https://doi.org/10.37538/0039-2383.2021.6.7.12 (rus)
3. Karaburc S.N., Yildizel S.A., Calis G.C. Evaluation of the basalt fiber reinforced pumice lightweight concrete. Magazine of Civil Engineering. 2020. № 2 (94). Pp. 81-92. DOI:https://doi.org/10.18720/MCE.94.7
4. Naumov A.E., Yudin D.A., Dolzhenko A.V., Prakhova A.A., Kucherenko A.S. Intellectualization of technological processes of construction and technical expertise [Intellektualizaciya tekhnologicheskih processov stroitel'no-tekhnicheskoj ekspertizy]. Bulletin of the Belgorod State Technological University named after V.G. Shukhov. 2022. No. 12. Pp. 28-38. DOI:https://doi.org/10.34031/2071-7318-2022-7-12-28-38 (rus)
5. Al-Hasnavi Ya.S.G., Laskov N.N., Efimov O.I., Zamaliev F.S. On the issue of designing a beam made of cellular concrete with rigid reinforcement. [K voprosu o proektirovanii balki iz yacheistogo betona s zhyostkoj armaturoj]. Regional architecture and construction. 2021. No. 3 (48). Pp. 137-143. (rus).
6. Efimov O., Salimov A. Stress-strain state prediction for statically indeterminate system with accounting for malfunctioning of rod elements production. IOP Conference series. Materials Science and Engineering. Kazan, Russia, 2020. 012067. DOIhttps://doi.org/10.1088/1757-899X/890/1/012067
7. Fedyuk R.S., Baranov A.V., Mugahed Amran Y.H. Effect of porous structure on sound absorption of cellular concrete. Construction Materials and Products. 2020. 3 (2). Pp. 5-18. DOI:https://doi.org/10.34031/2618-7183-2020-3-2-5-18
8. Kladieva P.V., Mozgovoy V.M., Moiseev M.V. Theoretical substantiation of increasing the efficiency of reinforcement of bent cellular concrete structures. [Teoreticheskoe obosnovanie povysheniya effektivnosti armirovaniya izgibaemyh yacheistobetonnyh konstrukcij]. Bulletin of BSTU named after V.G. Shukhov. 2021. No. 6. Pp. 27-35. DOIhttps://doi.org/10.34031/2071-7318-2021-6-6-27-35 (rus).
9. Al-hasnavi Ya.S.G. Investigation of the work of beams made of cellular concrete reinforced with light-steel thin-walled structures [Issledovanie raboty balok iz yacheistogo betona, armirovannyh legkimistal'nymi tonkostennymi konstrukciyami]. In the collection: Innovative methods of designing building structures of buildings and structures. collection of scientific papers of the All-Russian Scientific and Practical Conference. Southwestern State University. 2019. 11 p. (rus).
10. Kladieva P.V. Steel reinforcement bands of bent cellular concrete structures. [Stal'nye lenty armirovaniya izgibaemyh yacheistobetonnyh konstrukcij]. In the collection: VII International Student Construction Forum - 2022. Collection of reports of the VII International Student Construction Forum. Belgorod, 2022. Pp. 43-46. (rus).
11. Otsokov K.A. Innovative technologies in construction and their use in organizational and technological events. Construction Materials and Products. 2020. 3 (1). Pp. 7-13. DOI:https://doi.org/10.34031/2618-7183-2020-3-1-7-13
12. Kladieva P.V., Koshlich Yu.A. Improvement directions of technical regulations in the field of reinforced cellular concrete structures. Materials Science and Engineering. 2020. Vol. 945 012059. DOI:https://doi.org/10.1088/1757-899X/945/1/012059
13. Al-Hasnavi Ya.S.G., Laskov N.N., Efimov O.I., Zamaliev F.S. Coupling of rigid reinforcement and cellular concrete. [Cceplenie zhyostkoj armatury i yacheistogo betona]. Regional architecture and construction. 2021. No. 4 (49). Pp. 79-87. (rus)
14. Efimov O., Gimranov L., Fattakhova A. Calculations of the rigidity and the strength of concrete filled steel deck diaphragms. E3S Web of Conferences. 2021. Vol. 274. 3014. DOIhttps://doi.org/10.1051/e3sconf/202127403014
15. Varlamov A.A., Gavrilov B.V., Davydova A.M. Destruction model of idealized concrete structure by sawing. Construction Materials and Products. 2020. 3 (2). Pp. 46-54. DOI:https://doi.org/10.34031/2618-7183-2020-3-2-46-54














